git clone git://github.com/skeeto/perlin-noise.git
In short, Perlin noise is based on a grid of randomly-generated gradient vectors which describe how the arbitrarily-dimensional “surface” is sloped at that point. The noise at the grid points is always 0, though you’d never know it. When sampling the noise at some point between grid points, a weighted interpolation of the surrounding gradient vectors is calculated. Vectors are reduced to a single noise value by dot product.
Rather than waste time trying to explain it myself, I’ll link to an existing, great tutorial: The Perlin noise math FAQ. There’s also the original presentation by Ken Perlin, Making Noise, which is more concise but harder to grok.
When making my own implementation, I started by with Octave. It’s my “go to language” for creating a prototype when I’m doing something with vectors or matrices since it has the most concise syntax for these things. I wrote a two-dimensional generator and it turned out to be a lot simpler than I thought it would be!
Because it’s 2D, there are four surrounding grid points to consider
and these are all hard-coded. This leads to an interesting property:
there are no loops. The code is entirely vectorized, which makes it
quite fast. It actually keeps up with my generalized Java solution
(next) when given a grid of points, such as from meshgrid().
The grid gradient vectors are generated on the fly by a hash function. The integer x and y positions of the point are hashed using a bastardized version of Robert Jenkins’ 96 bit mix function (the one I used in my infinite parallax starfield) to produce a vector. This turned out to be the trickiest part to write, because any weaknesses in the hash function become very apparent in the resulting noise.
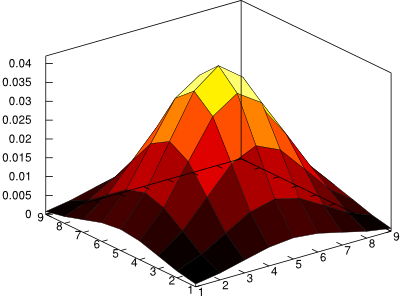
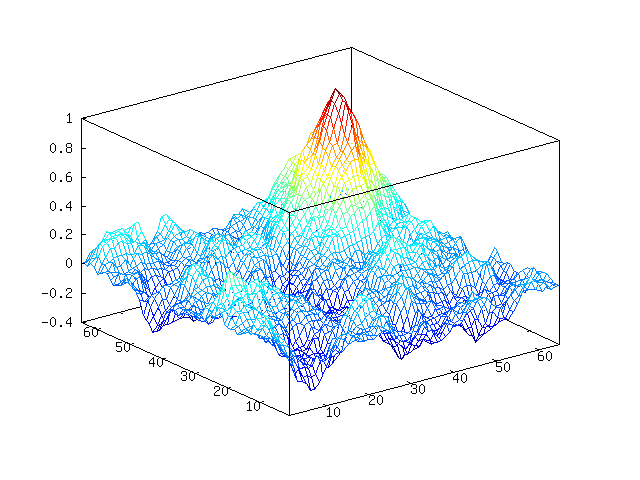
Using Octave, this took two seconds to generate on my laptop. You can’t really tell by looking at it, but, as with all Perlin noise, there is actually a grid pattern.

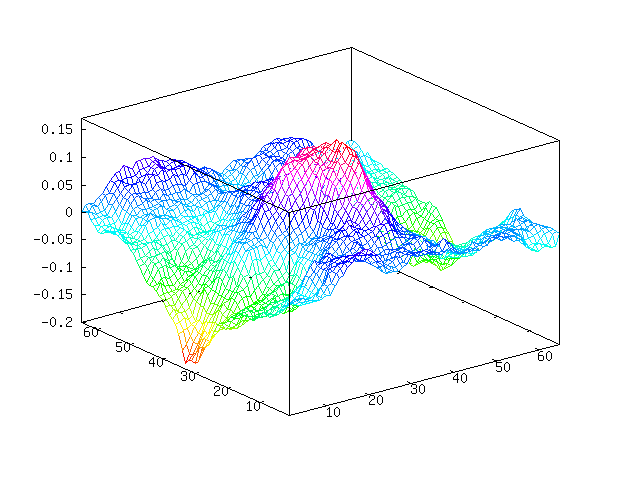
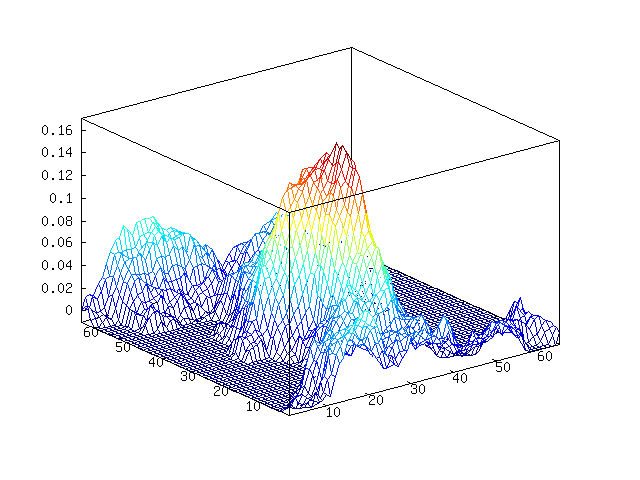
I then wrote a generalized version, perlin.m, that can generate
arbitrarily-dimensional noise. This one is a lot shorter, but it’s not
vectorized, can only sample one point at a time, and is incredibly
slow. For a hash function, I use Octave’s hashmd5(), so this one
won’t work in Matlab (which provides no hash function
whatsoever). However, it is a lot shorter!
%% Returns the Perlin noise value for an arbitrary point.
function v = perlin(p)
v = 0;
%% Iterate over each corner
for dirs = [dec2bin(0:(2 ^ length(p) - 1)) - 48]'
q = floor(p) + dirs'; % This iteration's corner
g = qgradient(q); % This corner's gradient
m = dot(g, p - q);
t = 1.0 - abs(p - q);
v += m * prod(3 * t .^ 2 - 2 * t .^ 3);
end
end
%% Return the gradient at the given grid point.
function v = qgradient(q)
v = zeros(size(q));
for i = 1:length(q);
v(i) = hashmd5([i q]) * 2.0 - 1.0;
end
end
It took Octave an entire day to generate this “fire” video, which is ridiculously long. An old graphics card could probably do this in real time.
This was produced by viewing a slice of 3D noise. For animation, the viewing area moves in two dimensions (z and y). One dimension makes the fire flicker, the other makes it look like it’s rising. A simple gradient was applied to the resulting noise to fade away towards the top.
I wanted to achieve this same effect faster, so next I made a generalized Java implementation, which is the bulk of the repository. I wrote my own Vector class (completely unlike Java’s depreciated Vector but more like Apache Commons Math’s RealVector), so it looks very similar to the Octave version. It’s much, much faster than the generalized Octave version. It doesn’t use a hash function for gradients — instead randomly generating them as needed and keeping track of them for later with a Map.
I wanted to go faster yet, so next I looked at OpenCL for the first time. OpenCL is an API that allows you to run C-like programs on your graphics processing unit (GPU), among other things. I was sticking to Java so I used lwjgl’s OpenCL bindings. In order to use this code you’ll need an OpenCL implementation available on your system, which, unfortunately, is usually proprietary. My OpenCL noise generator only generates 3D noise.
Why use the GPU? GPUs have a highly-parallel structure that makes them faster than CPUs at processing large blocks of data in parallel. This is really important when it comes to computer graphics, but it can be useful for other purposes as well, like generating Perlin noise.
I had to change my API a little to make this effective. Before, to generate noise samples, I passed points in individually to PerlinNoise. To properly parallelize this for OpenCL, an entire slice is specified by setting its width, height, step size, and z-level. This information, along with pre-computed grid gradients, is sent to the GPU.
This is all in the opencl branch in the repository. When run, it
will produce a series of slices of 3D noise in a manner similar to the
fire example above. For comparison, it will use the CPU by default,
generating a series of simple-*.png. Give the program one argument,
“opencl”, and it will use OpenCL instead, generating a series of
opencl-*.png. You should notice a massive increase in speed when
using OpenCL. In fact, it’s even faster than this. The vast majority
of the time is spent creating these output PNG images. When I disabled
image output for both, OpenCL was 200 times faster than the
(single-core) CPU implementation, still spending a significant amount
of time just loading data off the GPU.
And finally, I turned the OpenCL output into a video,
That’s pretty cool!
I still don’t really have a use for Perlin noise, especially not under constraints that require I use OpenCL to generate it. The big thing I got out of this project was my first experience with OpenCL, something that really is useful at work.
]]>