nullprogram.com/blog/2009/06/23/
Did you know that Emacs comes with a
calculator? Woop-dee-doo! Call the presses! Wow, a whole
calculator! Sounds a bit lame, right?
Actually, it's much more than just a simple calculator. It's a computer
algebra system! It is officially called a calculator, which isn't
fair. It's an understatement, and I am sure has caused many people to
overlook it. I finally ran into it during a thorough (re)reading of
the Emacs manuals and almost skipped over it myself.
Ever see that demonstration by Will Wright for the game Spore
several years ago? The player starts as a single-cell organism and
evolves into a civilization with interstellar presence. When he
started the demo he showed a cell through what looked like a
microscope. No one had any idea yet what the game was about, so every
time he increased the scope, from bacteria to animal, animal to
civilization, civilization to space travel, interplanetary travel to
interstellar travel, there was a huge reaction from the audience. It
was like those infomercials: "But that's not all!!!"
As I made my way through the Emacs calc manual I was continually
amazed by its power, with a similar constant increase in scope. Each
new page was almost saying, "But that's not all!!!"
Like an infomercial I'm going to run through some of its features. See
the calc manual for a real thorough introduction. It has practice
exercises that shows some gotchas and interesting feature
interactions.
Fire it up with C-x * c or M-x calc. There
will be two new windows (Emacs windows, that is), one with the
calculator and the other with usage history (the "trail").
First of all, the calculator operates on a stack and so its basic use
is done with RPN. The stack builds vertically, downwards. Type in
numbers and hit enter to push them onto the stack. Operators can be
typed right after the number, so no need to hit enter all the
time. Because negative (-) is reserved for subtraction an
underscore _ is used to type a negative number. An
example stack with 3, 4, and 10,
3: 3
2: 4
1: 10
.
10 is at the "top" of the stack (indicated by the "1:"), so if we type
a * the top two elements are multiplied. Like so,
2: 3
1: 40
.
The calculator has no limitations on the size of integers, so you work
with large numbers without losing precision. For example, we'll
take 2^200.
2: 2
1: 200
.
Apply the ^ operator,
1: 1606938044258990275541962092341162602522202993782792835301376
.
But that's not all!!! It has a complex number type, which is entered
in pairs (real, imaginary) with parenthesis. They can be operated on
like any other number. Take -1 + 2i minus 4 +
2i,
2: (-1, 2)
1: (4, 2)
.
Subtract with -,
1: -5
.
Then take the square root of that using Q, the square
root function.
1: (0., 2.2360679775)
.
We can set the calculator's precision with p. The default
is 12 places, showing here 1 / 7.
1: 0.142857142857
.
If we adjust the precision to 50 and do it again,
2: 0.142857142857
1: 0.14285714285714285714285714285714285714285714285714
.
Numbers can be displayed in various notations, too, like fixed-point,
scientific notation, and engineering notation. It will switch between
these without losing any information (the stored form is separate from
the displayed form).
But that's not all!!! We can represent rational numbers precisely with
ratios. These are entered with a :. Push
on 1/7, 3/14, and 17/29,
3: 1:7
2: 3:13
1: 17:29
.
And multiply them all together, which displays in the lowest form,
1: 51:2842
.
There is a mode for working in these automatically.
But that's not all!!! We can change the radix. To enter a number with
a different radix, which prefix it with the radix and a
#. Here is how we enter 29 in base-2,
2#11101
We can change the display radix with d r. With 29 on the
stack, here's base-4,
1: 4#131
.
Base-16,
1: 16#1D
.
Base-36,
1: 36#T
.
But that's not all!!! We can enter algebraic expressions onto the
stack with apostrophe, '. Symbols can be entered as part
of the expression. Note: these expressions are not entered in RPN.
1: a^3 + a^2 b / c d - a / b
.
There is a "big" mode (d B) for easier reading,
2
3 a b a
1: a + ---- - -
c d b
.
We can assign values to variables to have the expression evaluated. If
we assign a to 10 and use the "evaluates-to" operator,
2
3 a b a 100 b 10
1: a + ---- - - => 1000 + ----- - --
c d b c d b
.
But that's not all!!! There is a vector type for working with vectors
and matrices and doing linear algebra. They are entered with
brackets, [].
2: [4, 1, 5]
1: [ [ 1, 2, 3 ]
[ 4, 5, 6 ]
[ 6, 7, 8 ] ]
.
And take the dot product, then take cross product of this vector and matrix,
2: [38, 48, 58]
1: [ [ -14, -18, -22 ]
[ -19, -18, -17 ]
[ 15, 18, 21 ] ]
.
Any matrix and vector operator you could probably think of is
available, including map and reduce (and you can define your own
expression to apply).
We can use this to solve a linear system. Find x
and y in terms of a and b,
x + a y = 6
x + b y = 10
Enter it (note we are using symbols),
2: [6, 10]
1: [ [ 1, a ]
[ 1, b ] ]
.
And divide,
4 a 4
1: [6 + -----, -----]
a - b b - a
.
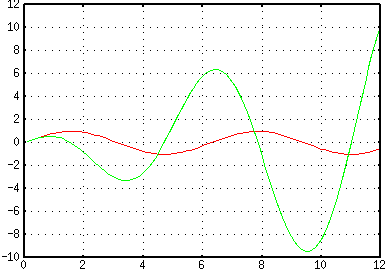
But that's not all!!! We can create graphs if gnuplot is installed. We
can give it two vectors, or an algebraic expression. This plot
of sin(x) and x cos(x) was made with just a
few keystrokes,
But that's not all!!! There is an HMS type for handling times and
angles. For 2 hours, 30 minutes, and 4 seconds, and some others,
3: 2@ 30' 4"
2: 4@ 22' 13"
1: 1@ 2' 56"
.
Of course, the normal operators work as expected. We can add them all up,
1: 7@ 55' 13"
.
We can convert between this and radians, and degrees, and so on.
But that's not all!!! The calculator also has a date type, entered
inside angled brackets, <> (in algebra entry
mode). It is really flexible on input dates. We can insert the current
date with t N.
1: <6:59:34pm Tue Jun 23, 2009>
.
If we add numbers they are treated as days. Add 4,
1: <6:59:34pm Sat Jun 27, 2009>
.
It works with the HMS format from before too. Subtract 2@ 3'
15".
1: <4:56:32pm Sat Jun 27, 2009>
.
But that's not all!!! There is a modulo form for performing modulo
arithmetic. For example, 17 mod 24,
1: 17 mod 24
.
Add 10,
1: 3 mod 24
.
This is most useful for forms such as n^p mod M, which
this will handle efficiently. For example, 3^100000 mod
24. The naive way would be to find 3^100000 first,
then take the modulus. This involves a computationally expensive
middle step of calculating 3^100000, a huge number. The
modulo form does it smarter.
But that's not all!!! The calculator can do unit conversions. The
version of Emacs (22.3.1) I am typing in right now knows about 159
different units. For example, I push 65 mph onto the stack,
1: 65 mph
.
Convert to meters per second with u c,
1: 29.0576 m / s
.
It is flexible about mixing type of units. For example, I enter 3
cubic meters,
3
1: 3 m
.
I can convert to gallons,
1: 792.516157074 gal
.
I work in a lab without Internet access during the day, so when I need
to do various conversions Emacs is indispensable.
The speed of light is also a unit. I can enter 1 c and
convert to meters per second,
1: 299792458 m / s
.
But that's not all!!! As I said, it's a computer algebra system so it
understands symbolic math. Remember those algebraic expressions from
before? I can operate on those. Let's push some expressions onto the
stack,
3: ln(x)
2 a x
2: a x + --- + c
b
1: y + c
.
Multiply the top two, then add the third,
2 a x
1: ln(x) + (a x + --- + c) (y + c)
b
.
Expand with a x, then simplify with a s,
2 a x y 2 a c x 2
1: ln(x) + a y x + ----- + c y + a c x + ----- + c
b b
.
Now, one of the coolest features: calculus. Differentiate with respect
to x, with a d,
1 a y a c
1: - + 2 a y x + --- + 2 a c x + ---
x b b
.
Or undo that and integrate it,
3 2 3 2
a y x a x y a c x a c x 2
1: x ln(x) - x + ------ + ------ + c x y + ------ + ------ + x c
3 2 b 3 2 b
.
That's just awesome! That's a text editor ... doing calculus!
So, that was most of the main features. It was kind of exhausting
going through all of that, and I am only scratching the surface of
what the calculator can do.
Naturally, it can be extended with some elisp. It provides a
defmath macro specifically for this.
I bet (hope?) someday it will have a functions for doing Laplace and
Fourier transforms.