nullprogram.com/blog/2009/08/28/
This is related to a project I am working on and will post here
soon. I imagine that, with a little more effort, this algorithm could
turn into a short amateur paper.
Suppose you want to use a computer to simulate the roll of two
six-sided dice (notated 2d6). The simplest approach would
be to replicate the results the same way you would roll dice:
independently and randomly generate two numbers between 1 and 6
inclusively. We easily can do this for any number of dice, we just
iterate and roll each die. Like this recursive function,
(defun roll (n sides)
"Roll n dice with given number of sides."
(if (zerop n) ()
(cons (1+ (random sides))
(roll (1- n) sides))))
However, generating a number between 1 and 6 wastes small amounts of
entropy. A six-sided die only takes about 2.58 bits of entropy to
generate. Since we can only use bits discretely we have to spend 3
bits, throwing out 0.42 bits. On top of that, when we pull out 3 bits
and they are out of range (0 or 7) we have to throw them out and try
again.
Let's say we wanted to roll 10 dice, or 100 dice, or 1000 dice? Do we
really need to generate that many numbers individually? That's a lot
of wasted entropy adding up, entropy which can be expensive to
gather. Well, we could instead use the probability distribution of
the roll so that only a single number needs to be generated.
For a 2d6 roll, there are 36 unique possible outcomes
(6^2). We could select a number between 0 and 35, then choose that
specific roll. This roll can be calculated with a series of division
and modulus operations (u for a number from a
uniform distribution) (also, note that the division is
integer division),
(defun roll-perm (n s u)
"Get uth permutation of n s-sided dice."
(if (zerop n) ()
(let ((perms (expt s (1- n))))
(cons (1+ (/ u perms))
(roll-perm (1- n) s (mod u perms))))))
If we're only interested in the sum, we could save memory by making
this tail recursive — or iterative — and summing the dice as we
calculate them. Ignoring the exponent, this is O(n), not
better than the simple algorithm in terms of growth rate. This
algorithm is more efficient when it comes to entropy, though.
Consider 3d6, with 216 possible outcomes, ideally with
the simple algorithm takes 3 3-bit rolls, consuming 9 bits. About 1.25
bits was not actually used (0.42 * 3). In the entropy-efficient
algorithm we need about 7.75 bits, so it only consumes 8 bits of
entropy. We saved a bit. That gap only gets larger with more dice. For
100d6 the simple algorithm uses 41 more bits than
necessary.
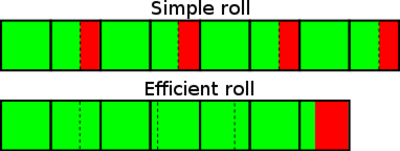
The efficient roll is basically defragmenting the individual rolls on
the entropy stream.
In non-ideal world, though, some cases don't work out well. In
12d6, almost half the numbers (compared to 25% in the
case of 1d6) from the uniform distribution will be out of range and a
lot more bits would be needed. On average, rolling dice individually
(or only some of them individually) for 12d6 will
be more efficient.
The efficient algorithm is only more efficient above a point near
where mod(log2(s), 1) < mod(log2(n^s), 1).
And, all of this doesn't come without a cost. You must pay the piper,
and this algorithm is paid with CPU and memory. Notice that exponent
there? That has to be done to exact precision (no floating point), and
it grows very quickly. If you want to roll more than a handful of
dice, you will be crunching some large numbers. Rolling just
100d6 means you have to work with a 78 digit
integer. 10000d6 is a 7782 digit integer. These can't be
done in floating point because the resolution of floating point is too
low: some rolls would not be possible.
The exponent could be memoized to
trade some of that CPU time for more memory usage. Still, pretty
costly. If you don't value your entropy, the tradeoff might not be
worth it.
I can't see a way around performing that calculation. We need to know
that big number exactly. Perhaps a mathematician might be able to
manipulate the formulas such that it's not so expensive.
If you're rolling lots of dice and you want to preserve binary
entropy, try it out. If you want to be really efficient queue up rolls
— or generate them ahead of time — so that the number of outcomes is
just below a power of two. In the case of d6, some good
number of dice to roll are 17 (~43.94 bits), 29 (~74.96), 41
(~105.983), 94 (~242.986 bits), 200 (~516.993), 253 (~653.995 bits),
306 (~791.99853 bits), and 971 (~2509.99859 bits). (Notice these get
closer and closer to an integer number of bits.)