A Seedable JavaScript PRNG

In preparation for my 7-day roguelike, I developed a seedable pseudo-random number generator library. Half of it is basically a port of BrianScheme’s PRNG.

JavaScript comes with an automatically-seeded global uniform PRNG, Math.random(). This is suitable for most purposes, but if repeatability and isolation is desired — such as when generating a roguelike dungeon — it’s inadequate. I also wanted to be able to sample from different probability distributions, particularly the normal distribution and the exponential distribution.

The underlying number generator is the elegant RC4. Seeds are strings and anything else (except functions) is run through JSON.stringify(). Characters above code 255 are treated as two-byte values. If no seed is provided it will grab some of the available entropy for the job. To generate a uniform random double-precision value, 7 bytes (56 bits) are generated to account for the full 53-bit mantissa.

All other distributions sample from the uniform number generator, so bits are twiddled in only one place. Moreso, it means that Math.random() can be used as the core random number generator. My RC4 implementation is about 10x slower than V8’s Math.random(), so if all you care about is the probability distributions, not the seeding, then you could benefit from better performance. Just provide Math.random as the “seed”.

Here’s an example of it in action. I’m seeding it with an arbitrary object and generating six normally-distributed values. The output should be exactly the same no matter what JavaScript engine is used.

(function(array, n) {
    var rng = new RNG({foo: 'bar'});
    for (var i = 0; i < n; i++) {
        array.push(parseFloat(rng.normal().toFixed(4)));
    }
    return array;
}([], 6));
// => [0.807, -0.9347, -1.4543, -0.2737, 0.5064, -1.7342]

Provided probability distributions:

• Uniform
• Normal
• Exponential
• Poisson
• Gamma

As far as the extras go, in my game I only ended up using the exponential distribution, for generating monster-spawning events. I intended to use the normal distribution for map generation, but, to save time, I used rot.js for that purpose.

As far as testing goes, I basically just exported the output to GNU Octave so that I could eyeball the histogram and do some basic statistical checks. Everything looks reasonable, so I assume it’s implemented correctly. “That’s the problem with randomness. You can never be sure.”

Using the same seed as above, here are some histograms of the first 10,000 samples for different probability distributions.

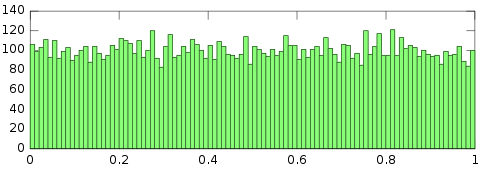
Uniform:

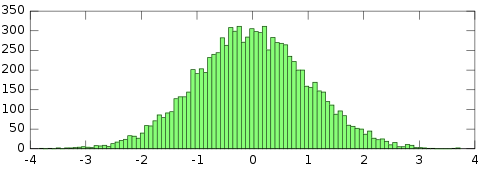
Normal:

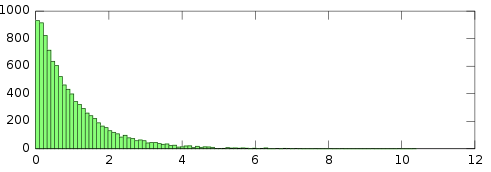
Exponential:

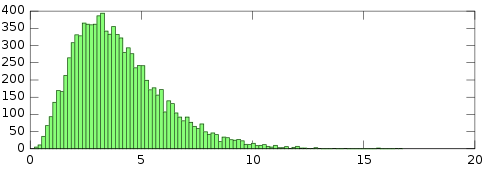
Gamma (mean = 4):

• javascript