nullprogram.com/blog/2016/09/15/
One of my favorite data processing tools is jq, a command line
JSON processor. It’s essentially awk for JSON. You supply a small
script composed of transformations and filters, and jq evaluates
the filters on each input JSON object, producing zero or more outputs
per input. My most common use case is converting JSON data into CSV
with jq’s @csv filter, which is then fed into SQLite (another
favorite) for analysis.
On a recent pass over the manual, the while and until
filters caught my attention, lighting up my
Turing-completeness senses. These filters allow jq to compute
an arbitrary recurrence, such as the Mandelbrot set.
Setting that aside for a moment, I said before that an input could
produce zero or more outputs. The zero is when it gets filtered out,
and one output is the obvious case. Some filters produce multiple
outputs from a single input. There are a number of situations when
this happens, but the important one is the range filter. For
example,
$ echo 6 | jq 'range(1; .)'
1
2
3
4
5
The . is the input object, and range is producing one output for
every number between 1 and . (exclusive). If an expression has
multiple filters producing multiple outputs, under some circumstances
jq will produce a Cartesian product: every combination is generated.
$ echo 4 | jq -c '{x: range(1; .), y: range(1; .)}'
{"x":1,"y":1}
{"x":1,"y":2}
{"x":1,"y":3}
{"x":2,"y":1}
{"x":2,"y":2}
{"x":2,"y":3}
{"x":3,"y":1}
{"x":3,"y":2}
{"x":3,"y":3}
So if my goal is the Mandelbrot set, I can use this to generate the
complex plane, over which I will run the recurrence. For input, I’ll
use a single object with the keys x, dx, y, and dy, defining
the domain and range of the image. A reasonable input might be:
{"x": [-2.5, 1.5], "dx": 0.05, "y": [-1.5, 1.5], "dy": 0.1}
The “body” of the until will be the Mandelbrot set
recurrence.
As you might expect, jq doesn’t have support for complex numbers, so
the components will be computed explicitly. I’ve worked it out
before, so borrowing that I finally had my script:
#!/bin/sh
echo '{"x": [-2.5, 1.5], "dx": 0.05, "y": [-1.5, 1.5], "dy": 0.1}' | \
jq -jr "{ \
ci: range(.y[0]; .y[1] + .dy; .dy), \
cr: range(.x[0]; .x[1]; .dx), \
k: 0, \
r: 0, \
i: 0, \
} | until(.r * .r + .i * .i > 4 or .k == 94; { \
cr,
ci,
k: (.k + 1),
r: (.r * .r - .i * .i + .cr),
i: (.r * .i * 2 + .ci) \
}) \
| [.k + 32] | implode"
It iterates to a maximum depth of 94: the number of printable ASCII
characters, except space. The final two filters convert the output
ASCII characters, and the -j and -r options tell jq to produce
joined, raw output. So, if you have jq installed and an exactly
80-character wide terminal, go ahead and run that script. You should
see something like this:
!!!!!!!!!!!!!!!!!!!"""""""""""""""""""""""""""""""""""""""""""""""""""
!!!!!!!!!!!!!!!!!"""""""""""""""""""""""""""""""""""""""""""""""""""""
!!!!!!!!!!!!!!!"""""""""""""""###########"""""""""""""""""""""""""""""
!!!!!!!!!!!!!!"""""""""#########################""""""""""""""""""""""
!!!!!!!!!!!!"""""""################$$$$$%3(%%$$$####""""""""""""""""""
!!!!!!!!!!!"""""################$$$$$$%%&'+)+J%$$$$####"""""""""""""""
!!!!!!!!!!"""################$$$$$$$%%%&()D8+(&%%$$$$#####""""""""""""
!!!!!!!!!""################$$$$$$$%%&&'(.~~~~2(&%%%%$$######""""""""""
!!!!!!!!""##############$$$$$$%%&'(((()*.~~~~-*)(&&&2%$$#####"""""""""
!!!!!!!""#############$$$$%%%%&&',J~0:~~~~~~~~~~4,./0/%$######""""""""
!!!!!!!"###########$$%%%%%%%&&&(.,^~~~~~~~~~~~~~~~~~4'&%$######"""""""
!!!!!!"#######$$$%%','''''''''(+4~~~~~~~~~~~~~~~~~~~1)3%$$######""""""
!!!!!!###$$$$$$%%%&'*04,-C-+))+8~~~~~~~~~~~~~~~~~~~~~/(&$$#######"""""
!!!!!!#$$$$$$%%%%&'(+2~~~~~~~/0~~~~~~~~~~~~~~~~~~~~~~?'%$$$######"""""
!!!!!!$$$$$&&&&'(,-.6~~~~~~~~~A~~~~~~~~~~~~~~~~~~~~~~(&%$$$######"""""
!!!!!!`ce~~ku{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~,('&%$$$#######""""
!!!!!!$$$$$&&&&'(,-.6~~~~~~~~~A~~~~~~~~~~~~~~~~~~~~~~(&%$$$######"""""
!!!!!!#$$$$$$%%%%&'(+2~~~~~~~/0~~~~~~~~~~~~~~~~~~~~~~?'%$$$######"""""
!!!!!!###$$$$$$%%%&'*04,-C-+))+8~~~~~~~~~~~~~~~~~~~~~/(&$$#######"""""
!!!!!!"#######$$$%%','''''''''(+4~~~~~~~~~~~~~~~~~~~1)3%$$######""""""
!!!!!!!"###########$$%%%%%%%&&&(.,^~~~~~~~~~~~~~~~~~4'&%$######"""""""
!!!!!!!""#############$$$$%%%%&&',J~0:~~~~~~~~~~4,./0/%$######""""""""
!!!!!!!!""##############$$$$$$%%&'(((()*.~~~~-*)(&&&2%$$#####"""""""""
!!!!!!!!!""################$$$$$$$%%&&'(.~~~~2(&%%%%$$######""""""""""
!!!!!!!!!!"""################$$$$$$$%%%&()D8+(&%%$$$$#####""""""""""""
!!!!!!!!!!!"""""################$$$$$$%%&'+)+L%$$$$####"""""""""""""""
!!!!!!!!!!!!"""""""################$$$$$%3(%%$$$####""""""""""""""""""
!!!!!!!!!!!!!!"""""""""#########################""""""""""""""""""""""
!!!!!!!!!!!!!!!"""""""""""""""###########"""""""""""""""""""""""""""""
!!!!!!!!!!!!!!!!!"""""""""""""""""""""""""""""""""""""""""""""""""""""
!!!!!!!!!!!!!!!!!!!"""""""""""""""""""""""""""""""""""""""""""""""""""
Tweaking the input parameters, it scales up nicely:
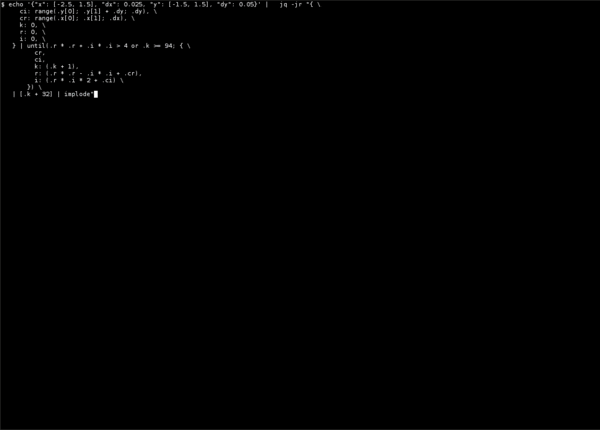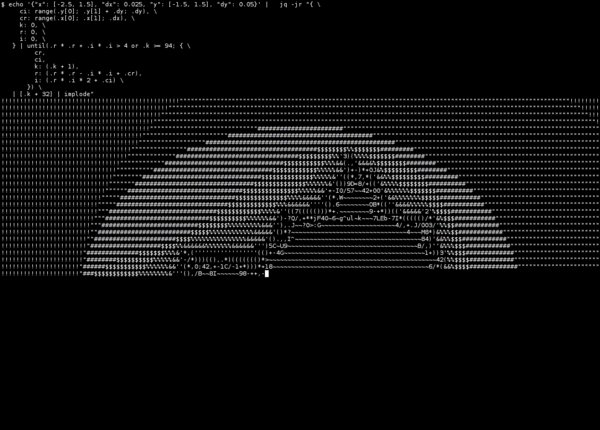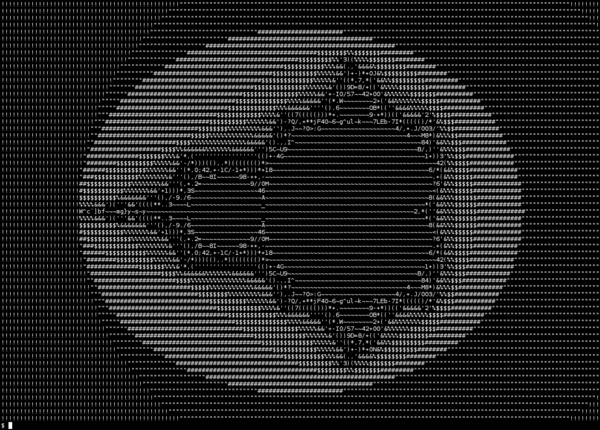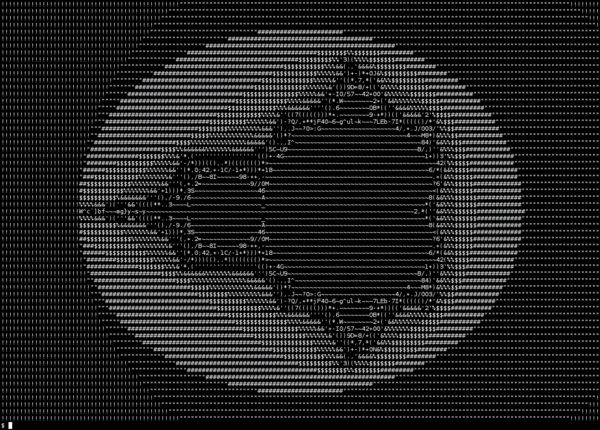

As demonstrated by the GIF, it’s very slow compared to more
reasonable implementations, but I wouldn’t expect otherwise. It
could be turned into a zoom animation just by feeding it more
input objects with different parameters. It will produce one full
“image” per input. Capturing an animation is left as an exercise for
the reader.