Neural Network Blackjack Game

Get the source code (C++):

• /download/neural.tar.gz (16.27KB)

This is a neural network I wrote for an artificial intelligence class I took about a year ago. It includes a stand alone neural network class you can easily use in your own C++ program. Built around this neural network is a simple version of Blackjack (hit or stand only). You can play the neural network at Blackjack after it has finished training, which can take up to a minute or so.

My implementation of the neural network is a really simple one, using only back propagation, but it still has some neat surprises in it. When I was working with it, I would use a simple GNU Octave script to watch what was going on in real time.

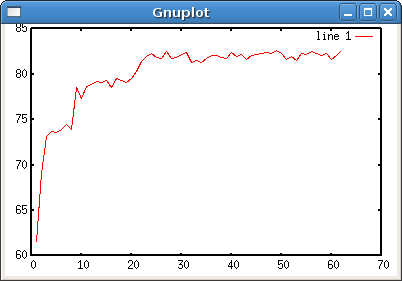
The x-axis is the number of iterations in tens of thousands and the y-axis describes how often the neural network plays exactly the same way a cheater would at the same seat. A cheater is defined as someone who knows what card is next and can play perfectly. Note: the neural network itself is not cheating. At the end, it agrees with the cheater about 83% of the time. This is the script that reads the neural network output. For those who don’t recognize the she-bang, save this to the file plotdat and set the execution permission (chmod +x plotdat).

#!/usr/bin/octave -qf
# Usage:
# plotdat filename [loop] [last index]

dat = dlmread(argv{1});
x = length(dat);
loop = 0;

if (length(argv) > 1)
  if (argv{2} == 'loop')
    loop = 1;
  else
    x = argv{2};
  end
end

plot(dat(1:x));

while(loop)
  dat = dlmread(argv{1});
  plot(dat);
  sleep(1);
end

pause;

When you run the program, a blank, dumb neural network is created. It doesn’t know how to play blackjack. In fact, just as it seems with my sister at times, it doesn’t know how to do anything at all. It’s like a newborn baby, but without any instincts. To make this neural network useful, it is taught to play blackjack by running it very quickly through about one million games, all tutored by a teacher who gets to cheat by looking ahead in the deck. This allows the teacher to always know the proper move.

The training works by giving the network an input and the desired output (determined by the cheating). The network adjusts its internal weights depending on the error between what its current output for the input and the desired output. In doing this, the neural network picks up on the statistical nature of its inputs and will pick up on patterns.

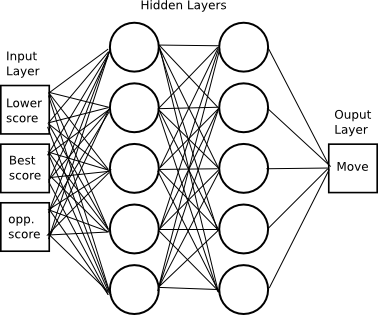
When setting up the neural network in your own program, the tricky part is determining how to encode the inputs so that patterns will be found. In this case, I provide 3 integers to the network: its lower bound score, its best score, and the visible opponent score. By lower bound and best score, I am talking about Aces. All aces are treated as 1’s in the lower bound and ideal (highest without bust) values in the best score. Scores never exceed 31, so we can encode this in 5 bits each for a total of 15 bits. We only need 1 output bit: hit (0) or stand (1). The network looks something like this, but with 30 hidden layer neurons and a lot more connections.

Here is an example run of the blackjack game,

Creating network ... created!
Training ...
Win, lose, total, c%, win%: 1536, 7640, 10000, 42.1168% , 15.36%
Win, lose, total, c%, win%: 3728, 14438, 20000, 55.8875% , 21.92%

... (lots of output for a few seconds) ...

Win, lose, total, c%, win%: 203744, 700338, 980000, 82.0455% , 20.3%
Win, lose, total, c%, win%: 205849, 707461, 990000, 82.5488% , 21.05%
Win, lose, total, c%, win%: 207981, 714515, 1000000, 82.3059% , 21.32%

Begin game:
Computer is dealt: (hole) 5
Computer is dealt: (hole) 5 4
Computer stands.
Your hand: 2 8
Hit? (y/n): y
Your hand: 2 8 3
Hit? (y/n): y
Your hand: 2 8 3 10
You bust with 23
Computer wins with 19 against your 23
Play again? (y/n) : y

Begin game:
Computer is dealt: (hole) 4
Computer is dealt: (hole) 4 10
Computer stands.
Your hand: 10 A
Hit? (y/n): n
Your hand: 10 A
You win with 21 against computer's 20
Play again? (y/n) : n

Computer wins, losses, push: 1 (50%), 1 (50%), 0 (0%)

If you decide to try using the neural network in your own program, be sure to play with different sized networks to see what works best. In my implementation, a small network would be 1 layer with 3 nodes and a large network would be 3 or 4 layers with hundreds of nodes. Bigger networks may not work well at all, and there is no way to know what size is best other than trial and error.

• ai