nullprogram.com/blog/2014/11/22/
When I was a kid I spent some time playing a top-down, 2D,
puzzle/action, 1993, MS-DOS game called God of Thunder. It
came on a shareware CD, now long lost, called Games People Play. A
couple decades later I was recently reminded of the game and decided
to dig it up and play it again. It’s not quite as exciting
as I remember it — nostalgia really warps perception — but it’s
still an interesting game nonetheless.
That got me thinking about how difficult it might be to modify (“mod”)
the game to add my own levels and puzzles. It’s a tiny game, so there
aren’t many assets to reverse engineer. Unpacked, the game just
barely fits on a 1.44 MB high density floppy disk. That was probably
one of the game’s primary design constraints. It also means it’s
almost certainly employing some sort of home-brew compression
algorithm in order to fit more content. I find these sorts of things
absolutely interesting and delightful.
You see, back in those old days, compression wasn’t really a “solved”
problem like it is today. They had to design and implement their own
algorithms, with varying degrees of success. Today if you
need compression for a project, you just grab zlib. Released
in 1995, it implements the most widely used compression algorithm
today, DEFLATE, with a tidy, in-memory API. zlib is well-tested,
thoroughly optimized, and sits in a nearly-perfect sweet spot between
compression ratio and performance. There’s even an embeddable
version. Since spinning platters are so slow compared to CPUs,
compression is likely to speed up an application simply because fewer
bytes need to go to and from the disk. Today it’s less about saving
storage space and more about reducing input/output demands.
Fortunately for me, someone has already reversed engineered
most of the God of Thunder assets. It uses its own flavor of
Lempel-Ziv-Storer-Szymanski (LZSS), which itself is derived
from LZ77, one of the algorithms used in DEFLATE. The original LZSS
paper focuses purely on the math, describing the algorithm in terms of
symbols with no concern for how it’s actually serialized into bits.
Those specific details were decided by the game’s developers, and
that’s what I’ll be describing below.
As an adult I’m finding the God of Thunder asset formats to be more
interesting than the game itself. It’s a better puzzle! I really
enjoy studying the file formats of various applications,
especially older ones that didn’t have modern standards to build on.
Usually lots of thought and engineering goes into the design these
formats — and, too often, not enough thought goes into it. The
format’s specifics reveal insights into the internal workings of the
application, sometimes exposing unanticipated failure modes. Prying
apart odd, proprietary formats (i.e. “data reduction”) is probably my
favorite kind of work at my day job, and it comes up fairly often.
God of Thunder LZSS Definition
An LZSS compression stream is made up of two kinds of chunks: literals
and back references. A literal chunk is passed through to the output
buffer unchanged. A reference chunk is a pair of numbers: a length and
an offset backwards into the output buffer. Only a single bit is
needed for each chunk to identify its type.
To avoid any sort of complicated and slow bit wrangling, the God of
Thunder developers (or whoever inspired them) came up with the smart
idea to stage 8 of these bits up at once as a single byte, a “control”
byte. Since literal chunks are 1 byte and reference chunks are 2
bytes, everything falls onto clean byte boundaries. Every group of 8
chunks is prefixed with one of these control bytes, and so every LZSS
compression stream begins with a control byte. The least significant
bit controls the 1st chunk in the group and the most significant bit
controls the 8th chunk. A 1 denotes a literal and a 0 denotes a
reference.
So, for example, a control byte of 0xff means to pass through
unchanged the next 8 bytes of the compression stream. This would be
the least efficient compression scenario, because the “compressed”
stream is 112.5% (9/8) bigger than the uncompressed stream. Gains come
entirely from the back references.
A back reference is two bytes little endian (this was in MS-DOS
running on x86), the lower 12 bits are the offset and the upper 4 bits
are the length, minus 2. That is, you read the 4 length bits and
add 2. This is because it doesn’t make any sense to reference a length
shorter than 2: a literal chunk would be shorter. The offset doesn’t
have anything added to it. This was a design mistake since an offset
of 0 doesn’t make any sense. It refers to a byte just outside the
output buffer. It should have been stored as the offset minus 1.
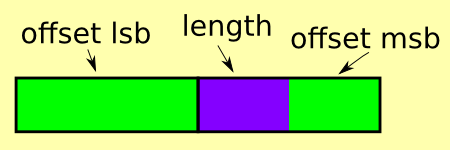
A 12-bit offset means up to a 4kB sliding window of output may be
referenced at any time. A 4-bit length, plus two, means up to 17 bytes
may be copied in a single back reference. Compared to other
compression algorithms, this is rather short.
It’s important to note that the length is allowed to extend beyond the
output buffer (offset < length). The bytes are, in effect, copied one
at a time into the output and may potentially be reused within the
same operation (like the opposite of memmove). An offset of
1 and a length of 10 means “repeat the last output byte 10 times.”
That’s the entire format! It’s extremely simple but reasonably
effective for the game’s assets.
Worst Case and Best Case
In the worst case, such as compressing random data, the compression
stream will be at most 112.5% (9/8) bigger than the uncompressed
stream.
In the best case, such as a long string of zeros, the compressed
stream will be, at minimum, 12.5% (1/8) the size of the decompressed
stream. Think about it this way: imagine every chunk is a reference of
maximum length. That’s 1 control byte plus 16 (8 * 2) reference
bytes, for a total of 17 compressed bytes. This emits 17 * 8
decompressed bytes, 17 being the maximum length from 8 chunks.
Conveniently those two 17s cancel, leaving a factor of 8 for the best
case.
LZSS End of Stream
If you’re paying really close attention, you may have noticed that
by grouping 8 control bits at a time, the length of the input stream
is, strictly speaking, constrained to certain lengths. What if, during
compression, the input stream stream comes up short of exactly those 8
chunks? As is, there’s no way to communicate a premature end to the
stream. There are three ways around this using a small amount of
metadata, each differing in robustness.
-
Keep track of the size of the decompressed data. When that many
bytes have been emitted, halt. This is how God of Thunder handles
it. A small validation check could be performed here. The output
stream should always end between chunks, not in the middle of a
chunk (i.e. in the middle of copying a back reference). Some of the
bits in the control byte may contain arbitrary data that doesn’t
effect the output, which is a concern when hashing compressed data.
My suggestion: require the unused control bits to be 0, which
allows for an additional validation check. The output stream should
never end just short of a literal chunk.
-
Keep track of the size of the compressed data. Halt when no more
chunks are encountered. A similar, weaker validation check can be
performed here: the input stream should never stop between two
bytes of a reference. It’s weaker because it’s less sensitive to
corruption, making it harder to detect. The same unused control bit
padding situation applies here.
-
Use an out-of-band end marker (EOF). This is very similar to
keeping track of the input size (the filesystem is doing it), but
has the weakest validation of all. The stream could be accidentally
truncated at any point between chunks, which is undetectable. This
makes it the least sensitive to corruption.
An LZSS Quine
After spending some time playing around with this format, I thought
about what it would take to make an LZSS quine. That is, find an
LZSS compressed stream that decompresses to itself. It’s been done
for DEFLATE, which I imagine is a much harder problem. There are zip
files containing exact copies of themselves, recursively. I’m
pretty confident it’s never been done for this exact compression
format, simply because it’s so specific to this old MS-DOS game.
I haven’t figured it out yet, so you won’t find the solution here.
This, dear readers, is my challenge to you! Using the format
described above, craft an LZSS quine. LZSS doesn’t have no-op chunks
(i.e. length = 0), which makes this harder than it would otherwise be.
It may not even be possible, which, in that case, your challenge is to
prove it!
So far I’ve determined that it begins with at least 4kB of 0xff. Why
is this? First, as I mentioned, all compression streams begin with a
control byte. Second, no references can be made until at least one
literal byte has been passed, so the first bit (LSB) of the first byte
is a 1, and the second byte is exactly the same as the first byte. So
the first two bytes are xxxxxx1, with the x being “don’t care (yet).”
If the next chunk is a back reference, those first two bytes become
xxxxxx01. It could only reference that one byte (so offset = 1), and
the length would need to be at least two, ensuring at least the first
three bytes of output all have that same pattern. However, on the most
significant byte of the reference chunk, this conflicts with having an
offset of 1 because the 9th bit of the offset is set to 1, forcing the
offset to an invalid 257 bytes. Therefore, the second chunk must be a
literal.
This pattern continues until the first eight chunks are all literals,
which means the quine begins with at least 9 0xff bytes. Going on,
this also means the first back reference is going to be 0xffff
(offset = 4095, length = 17), so the sliding window needs to be filled
enough to make that a offset valid. References would then be used to
“catch up” with the compression stream, then some magic is needed to
finish off the stream.
That’s where I’m stuck.