The 3n + 1 Conjecture

The 3n + 1 conjecture, also known as the Collatz conjecture, is based around this recursive function,

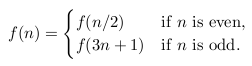
The conjecture is this,

This process will eventually reach the number 1, regardless of which positive integer is chosen initially.

The way I am defining this may not be entirely accurate, as I took a shortcut to make it a bit simpler. I am not a mathematician (IANAM) — but sometimes I pretend to be one. For a really solid definition, click through to the Wikipedia article in the link above.

A sample run, starting at 7, would look like this: 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1. The sequence starting at 7 contains 17 numbers. So 7 has a cycle-length of 17. Currently, there is no known positive integer that does not eventually lead to 1. If the conjecture is true, then none exists to be found.

I first found out about the problem when I saw it on UVa Online Judge. UVa Online Judge is a system that has a couple thousand programming problems to do. Users can submit solution programs written in C, C++, Java, or Pascal. For normal submissions, the fastest program wins.

Anyway, the way UVa Online Judge runs this problem is by providing the solution program pairs of integers on stdin as text. The integers define an inclusive range of integers over which the program must return the length of the longest Collatz cycle-length for all the integers inside that range. They don't tell you which ranges they are checking, except that all integers will be less than 1,000,000 and the sequences will never overflow a 32-bit integer (allowing shortcuts to be made to increase performance).

The simple approach would be defining a function that returns the cycle length (Lua programming language),

function collatz_len (n)
   local c = 1

   while n > 1 do
      c = c + 1
      if math.mod(n, 2) == 0 then
         n = n / 2
      else
         n = 3 * n + 1
      end
   end

   return c
end

Then we have a function check over a range (assuming n <= m here),

function check_range (n, m)
   local largest = 0

   for i = n, m do
      local len = collatz_len (i)

      if len > largest then
         largest = len
      end

   end

   return largest
end

And top it off with the i/o. (I am just learning Lua, so I hope I did this part properly!)

while not io.stdin.eof do
   n, m = io.stdin:read("*number", "*number")

   -- check for eof
   if n == nil or m == nil then
      break
   end

   print (n .. " " .. m .. " " .. check_range(n, m))
end

Notice anything extremely inefficient? We are doing the same work over and over again! Take, for example, this range: 7, 22. When we start with 7, we get the sequence shown above: 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1. Eight of these numbers are part of the range that we are looking at. When we get up to 22, we are going to walk down the same range again, less the 7. To make things more efficient, we apply some dynamic programming and store previous calculated cycle-lengths in an array. Once we get to a value we already calculated, we just look it up.

I used dynamic programming in my submission, which I wrote up in C. You can grab my source here. It fills in a large array (1000000 entries) as values are found, so no cycle-length is calculated twice. When I submitted this program, it ranked 60 out of about 300,000 entries. There are probably a number of tweaks that can increase performance, such as increasing the size of the array, but I didn't care much about inching closer to the top. I would bet that the very top entries did some trial-and-error and determined what ranges are tested, using the results to seed their program accordingly. You could take my code and submit it yourself, but that wouldn't be very honest, would it?

So why am I going through all of this describing such a simple problem? Well, it is because of this neat feature of Lua that applies well to this problem. Lua is kind of like Lisp. In Lisp, everything is a list ("list processing" --> Lisp). In Lua, (almost) everything is an associative array (Maybe they should have called it Assp? Or Hashp? I am kidding.) An object is a hash with fields containing function references. There is even some syntactic sugar to help this along.

The cool thing is that we can create a hash with default entries that reference a function that calculates the Collatz cycle-length of its key. Once the cycle-length is calculated, the function reference is replaced with the value, so the function is never called again from that point. The function only actually determines the next integer, then references the hash to get the cycle-length of that next integer.

Now this hash looks like it is infinitely large. This is really a form of lazy evaluation: no values are calculated until they are needed (this is one of my favorite things about Haskell). We don't need to explicitly ask for it to be calculated, either. We just go along looking up values in the array as if they were always there. Here is how you do it,

collatz_len = { 1 }

setmetatable (collatz_len, {
   __index = function (name, n)
      if (math.mod (n, 2) == 0) then
         name[n] = name[n/2] + 1;
      else
         name[n] = name[3 * n + 1] + 1;
      end
         return name[n]
   end
})

So we replace the collatz_len function with this array (and replace the call to an array reference) and we have applied dynamic programming to our old program. If I run the two programs with this sample input,

10 1000
1000 3000
300 500

and look at average running times, the dynamic programming version runs 87% faster than the original.

One problem with this, though, is the use of recursion. In Lua, it is really easy to hit recursion limits. For example, accessing element 10000 will cause the program to crash. This will probably get fixed someday, or in some implementation of Lua.

I thought there might be a way to do this in Perl, by changing the default hash value from undef to something else, but I was mildly disappointed to find out that this is not true.

Here is the source for the original program and the one with dynamic programming (BSD licenced): collatz_simple.lua and collatz.lua

• c
• lua