nullprogram.com/blog/2014/06/22/
Last time I demonstrated how to run Conway’s Game of Life
entirely on a graphics card. This concept can be generalized to any
cellular automaton, including automata with more than two states. In
this article I’m going to exploit this to solve the shortest path
problem for two-dimensional grids entirely on a GPU. It will be
just as fast as traditional searches on a CPU.
The JavaScript side of things is essentially the same as before — two
textures with fragment shader in between that steps the automaton
forward — so I won’t be repeating myself. The only parts that have
changed are the cell state encoding (to express all automaton states)
and the fragment shader (to code the new rules).
Included is a pure JavaScript implementation of the cellular
automaton (State.js) that I used for debugging and experimentation,
but it doesn’t actually get used in the demo. A fragment shader
(12state.frag) encodes the full automaton rules for the GPU.
Maze-solving Cellular Automaton
There’s a dead simple 2-state cellular automaton that can solve any
perfect maze of arbitrary dimension. Each cell is either OPEN or a
WALL, only 4-connected neighbors are considered, and there’s only one
rule: if an OPEN cell has only one OPEN neighbor, it becomes a WALL.

On each step the dead ends collapse towards the solution. In the above
GIF, in order to keep the start and finish from collapsing, I’ve added
a third state (red) that holds them open. On a GPU, you’d have to do
as many draws as the length of the longest dead end.
A perfect maze is a maze where there is exactly one solution. This
technique doesn’t work for mazes with multiple solutions, loops, or
open spaces. The extra solutions won’t collapse into one, let alone
the shortest one.

To fix this we need a more advanced cellular automaton.
Path-solving Cellular Automaton
I came up with a 12-state cellular automaton that can not only solve
mazes, but will specifically find the shortest path. Like above, it
only considers 4-connected neighbors.
- OPEN (white): passable space in the maze
- WALL (black): impassable space in the maze
- BEGIN (red): starting position
- END (red): goal position
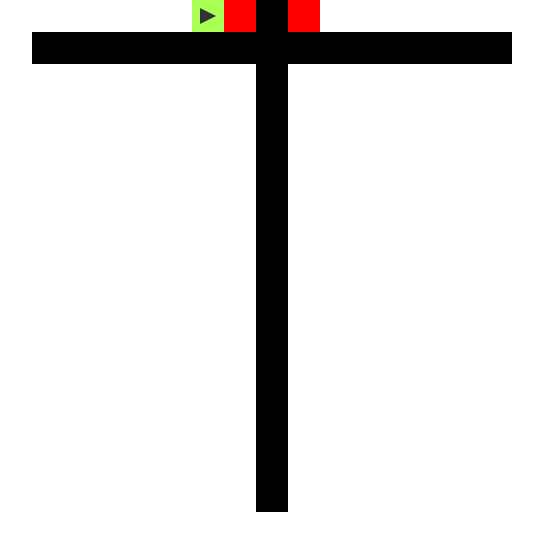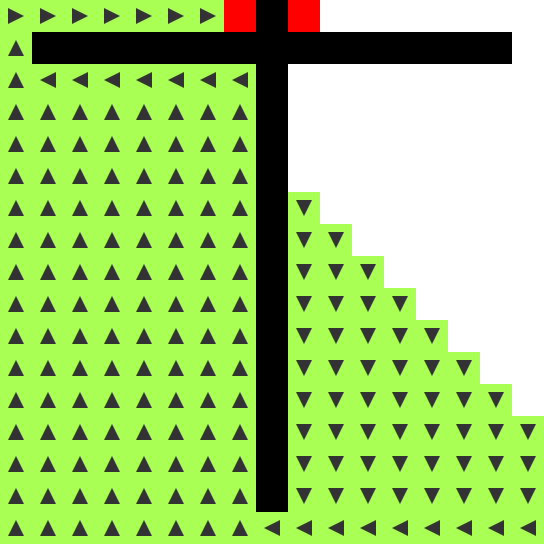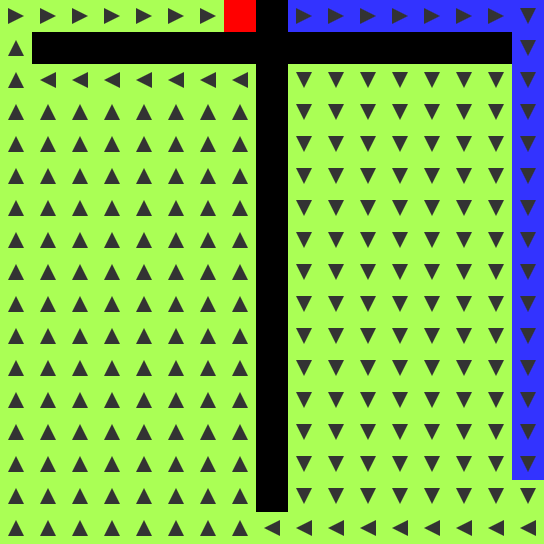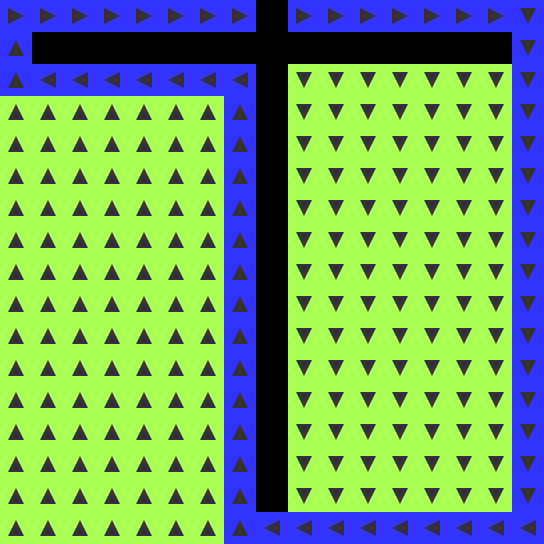
- FLOW (green): flood fill that comes in four flavors: north, east, south, west
- ROUTE (blue): shortest path solution, also comes in four flavors
If we wanted to consider 8-connected neighbors, everything would be
the same, but it would require 20 states (n, ne, e, se, s, sw, w, nw)
instead of 12. The rules are still pretty simple.
- WALL and ROUTE cells never change state.
- OPEN becomes FLOW if it has any adjacent FLOW cells. It points
towards the neighboring FLOW cell (n, e, s, w).
- END becomes ROUTE if adjacent to a FLOW cell. It points towards the
FLOW cell (n, e, s, w). This rule is important for preventing
multiple solutions from appearing.
- FLOW becomes ROUTE if adjacent to a ROUTE cell that points towards
it. Combined with the above rule, it means when a FLOW cell touches
a ROUTE cell, there’s a cascade.
- BEGIN becomes ROUTE when adjacent to a ROUTE cell. The direction is
unimportant. This rule isn’t strictly necessary but will come in
handy later.
This can be generalized for cellular grids of any arbitrary dimension,
and it could even run on a GPU for higher dimensions, limited
primarily by the number of texture uniform bindings (2D needs 1
texture binding, 3D needs 2 texture bindings, 4D needs 8 texture
bindings … I think). But if you need to find the shortest path along
a five-dimensional grid, I’d like to know why!
So what does it look like?

FLOW cells flood the entire maze. Branches of the maze are search in
parallel as they’re discovered. As soon as an END cell is touched, a
ROUTE is traced backwards along the flow to the BEGIN cell. It
requires double the number of steps as the length of the shortest
path.
Note that the FLOW cell keep flooding the maze even after the END was
found. It’s a cellular automaton, so there’s no way to communicate to
these other cells that the solution was discovered. However, when
running on a GPU this wouldn’t matter anyway. There’s no bailing out
early before all the fragment shaders have run.
What’s great about this is that we’re not limited to mazes whatsoever.
Here’s a path through a few connected rooms with open space.
Maze Types
The worst-case solution is the longest possible shortest path. There’s
only one frontier and running the entire automaton to push it forward
by one cell is inefficient, even for a GPU.

The way a maze is generated plays a large role in how quickly the
cellular automaton can solve it. A common maze generation algorithm
is a random depth-first search (DFS). The entire maze starts out
entirely walled in and the algorithm wanders around at random plowing
down walls, but never breaking into open space. When it comes to a
dead end, it unwinds looking for new walls to knock down. This methods
tends towards long, winding paths with a low branching factor.
The mazes you see in the demo are Kruskal’s algorithm mazes. Walls are
knocked out at random anywhere in the maze, without breaking the
perfect maze rule. It has a much higher branching factor and makes for
a much more interesting demo.
Skipping the Route Step
On my computers, with a 1023x1023 Kruskal maze it’s about an
order of magnitude slower (see update below) than A*
(rot.js’s version) for the same maze. Not very
impressive! I believe this gap will close with time, as GPUs
become parallel faster than CPUs get faster. However, there’s
something important to consider: it’s not only solving the shortest
path between source and goal, it’s finding the shortest path between
the source and any other point. At its core it’s a breadth-first
grid search.
Update: One day after writing this article I realized that
glReadPixels was causing a gigantic bottlebeck. By only checking for
the end conditions once every 500 iterations, this method is now
equally fast as A* on modern graphics cards, despite taking up to an
extra 499 iterations. In just a few more years, this technique
should be faster than A*.
Really, there’s little use in ROUTE step. It’s a poor fit for the GPU.
It has no use in any real application. I’m using it here mainly for
demonstration purposes. If dropped, the cellular automaton would
become 6 states: OPEN, WALL, and four flavors of FLOW. Seed the source
point with a FLOW cell (arbitrary direction) and run the automaton
until all of the OPEN cells are gone.
Detecting End State
The ROUTE cells do have a useful purpose, though. How do we know when
we’re done? We can poll the BEGIN cell to check for when it becomes a
ROUTE cell. Then we know we’ve found the solution. This doesn’t
necessarily mean all of the FLOW cells have finished propagating,
though, especially in the case of a DFS-maze.
In a CPU-based solution, I’d keep a counter and increment it every
time an OPEN cell changes state. The the counter doesn’t change after
an iteration, I’m done. OpenGL 4.2 introduces an atomic
counter that could serve this role, but this isn’t available in
OpenGL ES / WebGL. The only thing left to do is use glReadPixels to
pull down the entire thing and check for end state on the CPU.
The original 2-state automaton above also suffers from this problem.
Encoding Cell State
Cells are stored per pixel in a GPU texture. I spent quite some time
trying to brainstorm a clever way to encode the twelve cell states
into a vec4 color. Perhaps there’s some way to exploit
blending to update cell states, or make use of some other kind
of built-in pixel math. I couldn’t think of anything better than a
straight-forward encoding of 0 to 11 into a single color channel (red
in my case).
int state(vec2 offset) {
vec2 coord = (gl_FragCoord.xy + offset) / scale;
vec4 color = texture2D(maze, coord);
return int(color.r * 11.0 + 0.5);
}
This leaves three untouched channels for other useful information. I
experimented (uncommitted) with writing distance in the green channel.
When an OPEN cell becomes a FLOW cell, it adds 1 to its adjacent FLOW
cell distance. I imagine this could be really useful in a real
application: put your map on the GPU, run the cellular automaton a
sufficient number of times, pull the map back off (glReadPixels),
and for every point you know both the path and total distance to the
source point.
As mentioned above, I ran the GPU maze-solver against A* to test its
performance. I didn’t yet try running it against Dijkstra’s algorithm
on a CPU over the entire grid (one source, many destinations). If I
had to guess, I’d bet the GPU would come out on top for grids with a
high branching factor (open spaces, etc.) so that its parallelism is
most effectively exploited, but Dijkstra’s algorithm would win in all
other cases.
Overall this is more of a proof of concept than a practical
application. It’s proof that we can trick OpenGL into solving mazes
for us!