Improving on QBasic's Random Number Generator

November 17, 2020

nullprogram.com/blog/2020/11/17/

This article was discussed on Hacker News.

Pixelmusement produces videos about MS-DOS games and software. Each video ends with a short, randomly-selected listing of financial backers. In ADG Filler #57, Kris revealed the selection process, and it absolutely fits the channel’s core theme: a QBasic program. His program relies on QBasic’s built-in pseudo random number generator (PRNG). Even accounting for the platform’s limitations, the PRNG is much poorer quality than it could be. Let’s discuss these weaknesses and figure out how to make the selection more fair.

Kris’s program seeds the PRNG with the system clock (RANDOMIZE TIMER, a QBasic idiom), populates an array with the backers represented as integers (indices), continuously shuffles the list until the user presses a key, then finally prints out a random selection from the array. Here’s a simplified version of the program (note: QBasic comments start with apostrophe '):

CONST ntickets = 203  ' input parameter
CONST nresults = 12

RANDOMIZE TIMER

DIM tickets(0 TO ntickets - 1) AS LONG
FOR i = 0 TO ntickets - 1
    tickets(i) = i
NEXT

CLS
PRINT "Press any key to stop shuffling..."
DO
    i = INT(RND * ntickets)
    j = INT(RND * ntickets)
    SWAP tickets(i), tickets(j)
LOOP WHILE INKEY$ = ""

FOR i = 0 to nresults - 1
    PRINT tickets(i)
NEXT

This should be readable even if you don’t know QBasic. Note: In the real program, backers at higher tiers get multiple tickets in order to weight the results. This is accounted for in the final loop such that nobody appears more than once. It’s mostly irrelevant to the discussion here, so I’ve omitted it.

The final result is ultimately a function of just three inputs:

The system clock (TIMER)
The total number of tickets
The number of loop iterations until a key press

The second item has the nice property that by becoming a backer you influence the result.

QBasic RND

QBasic’s PRNG is this 24-bit Linear Congruential Generator (LCG):

uint32_t
rnd24(uint32_t *s)
{
    *s = (*s*0xfd43fd + 0xc39ec3) & 0xffffff;
    return *s;
}

The result is the entire 24-bit state. RND divides this by 2^24 and returns it as a single precision float so that the caller receives a value between 0 and 1 (exclusive).

Needless to say, this is a very poor PRNG. The LCG constants are reasonable, but the choice to limit the state to 24 bits is strange. According to the QBasic 16-bit assembly (note: the LCG constants listed here are wrong), the implementation is a full 32-bit multiply using 16-bit limbs, and it allocates and writes a full 32 bits when storing the state. As expected for the 8086, there was nothing gained by using only the lower 24 bits.

To illustrate how poor it is, here’s a randogram for this PRNG, which shows obvious structure. (This is a small slice of a 4096x4096 randogram where each of the 2^23 24-bit samples is plotted as two 12-bit coordinates.)

Admittedly this far overtaxes the PRNG. With a 24-bit state, it’s only good for 4,096 (2^12) outputs, after which it no longer follows the birthday paradox: No outputs are repeated even though we should start seeing some. However, as I’ll soon show, this doesn’t actually matter.

Instead of discarding the high 8 bits — the highest quality output bits — QBasic’s designers should have discarded the low 8 bits for the output, turning it into a truncated 32-bit LCG:

uint32_t
rnd32(uint32_t *s)
{
    *s = *s*0xfd43fd + 0xc39ec3;
    return *s >> 8;
}

This LCG would have the same performance, but significantly better quality. Here’s the randogram for this PRNG, and it is also heavily overtaxed (more than 65,536, 2^16 outputs).

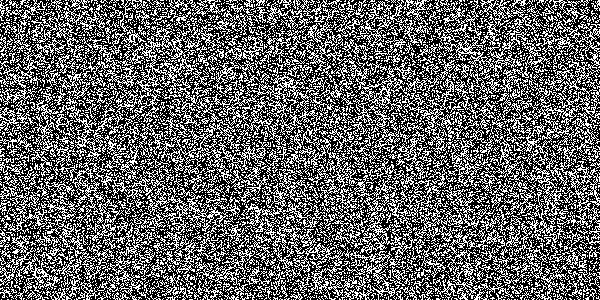
It’s a solid upgrade, completely for free!

QBasic RANDOMIZE

That’s not the end of our troubles. The RANDOMIZE statement accepts a double precision (i.e. 64-bit) seed. The high 16 bits of its IEEE 754 binary representation are XORed with the next highest 16 bits. The high 16 bits of the PRNG state is set to this result. The lowest 8 bits are preserved.

To make this clearer, here’s a C implementation, verified against QBasic 7.1:

uint32_t s;

void
randomize(double seed)
{
    uint64_t x;
    memcpy(&x ,&seed, 8);
    s = (x>>24 ^ x>>40) & 0xffff00 | (s & 0xff);
}

In other words, RANDOMIZE only sets the PRNG to one of 65,536 possible states.

As the final piece, here’s how RND is implemented, also verified against QBasic 7.1:

float
rnd(float arg)
{
    if (arg < 0) {
        memcpy(&s, &arg, 4);
        s = (s & 0xffffff) + (s >> 24);
    }
    if (arg != 0.0f) {
        s = (s*0xfd43fd + 0xc39ec3) & 0xffffff;
    }
    return s / (float)0x1000000;
}

System clock seed

The TIMER function returns the single precision number of seconds since midnight with ~55ms precision (i.e. the 18.2Hz timer interrupt counter). This is strictly time of day, and the current date is not part of the result, unlike, say, the unix epoch.

This means there are only 1,572,480 distinct values returned by TIMER. That’s small even before considering that these map onto only 65,536 possible seeds with RANDOMIZE — all of which are fortunately realizable via TIMER.

Of the three inputs to random selection, this first one is looking pretty bad.

Loop iterations

Kris’s idea of continuously mixing the array until he presses a key makes up for much of the QBasic PRNG weaknesses. He lets it run for over 200,000 array swaps — traversing over 2% of the PRNG’s period — and the array itself acts like an extended PRNG state, supplementing the 24-bit RND state.

Since iterations fly by quickly, the exact number of iterations becomes another source of entropy. The results will be quite different if it runs 214,600 iterations versus 273,500 iterations.

Possible improvement: Only exit the loop when a certain key is pressed. If any other key is pressed then that input and the TIMER are mixed into the PRNG state. Mashing the keyboard during the loop introduces more entropy.

Replacing the PRNG

Since the built-in PRNG is so poor, we could improve the situation by implementing a new one in QBasic itself. The challenge is that QBasic has no unsigned integers, not even unsigned integer operators (i.e. Java and JavaScript’s >>>), and signed overflow is a run-time error. We can’t even re-implement QBasic’s own LCG without doing long multiplication in software, since the intermediate result overflows its 32-bit LONG.

Popular choices in these constraints are Park–Miller generator (as we saw in Bash) or a lagged Fibonacci generator (as used by Emacs, which was for a long time constrained to 29-bit integers).

However, I have a better idea: a PRNG based on RC4. Specifically, my own design called Sponge4, a sponge construction built atop RC4. In short: Mixing in more input is just a matter of running the key schedule again. Implementing this PRNG requires just two simple operations: modular addition over 2^8, and array swap. QBasic has a SWAP statement, so it’s a natural fit!

Sponge4 (RC4) has much higher quality output than the 24-bit LCG, and I can mix in more sources of entropy. With its 1,700-bit state, it can absorb quite a bit of entropy without loss.

Learning QBasic

Until this past weekend, I had not touched QBasic for about 23 years and had to learn it essentially from scratch. Though within a couple of hours I probably already understood it better than I ever had. That’s in large part because I’m far more experienced, but also probably because QBasic tutorials are universally awful. Not surprisingly they’re written for beginners, but they also seem to be all written by beginners, too. I soon got the impression that QBasic community has usually been another case of the blind leading the blind.

There’s little direct information for experienced programmers, and even the official documentation tends to be thin in important places. I wanted documentation that started with the core language semantics:

The basic types are INTEGER (int16), LONG (int32), SINGLE (float32), DOUBLE (float64), and two flavors of STRING, fixed-width and variable-width. Late versions also had incomplete support for a 64-bit, 10,000x fixed-point CURRENCY type.
Variables are SINGLE by default and do not need to be declared ahead of time. Arrays have 11 elements by default.
Variables, constants, and functions may have a suffix if their type is not SINGLE: INTEGER %, LONG &, SINGLE !, DOUBLE #, STRING $, and CURRENCY @. For functions, this is the return type.
Each variable type has its own namespace, i.e. i% is distinct from i&. Arrays are also their own namespace, i.e. i% is distinct from i%(0) is distinct from i&(0).
Variables may be declared explicitly with DIM. Declaring a variable with DIM allows the suffix to be omitted. It also locks that name out of the other type namespaces, i.e. DIM i AS LONG makes any use of i% invalid in that scope. Though arrays and scalars can still have the same name even with DIM declarations.
Numeric operations with mixed types implicitly promote like C.
Functions and subroutines have a single, common namespace regardless of function suffix. As a result, the suffix can (usually) be omitted at function call sites. Built-in functions are special in this case.
Despite initial appearances, QBasic is statically-typed.
The default is pass-by-reference. Use BYVAL to pass by value.
In array declarations, the parameter is not the size but the largest index. Multidimensional arrays are supported. Arrays need not be indexed starting at zero (e.g. (x TO y)), though this is the default.
Strings are not arrays, but their own special thing with special accessor statements and functions.
Scopes are module, subroutine, and function. “Global” variables must be declared with SHARED.
Users can define custom structures with TYPE. Functions cannot return user-defined types and instead rely on pass-by-reference.
A crude kind of dynamic allocation is supported with REDIM to resize $DYNAMIC arrays at run-time. ERASE frees allocations.

These are the semantics I wanted to know getting started. Throw in some illustrative examples, and then it’s a tutorial for experienced developers. (Future article perhaps?) Anyway, that’s enough to follow along below.

Implementing Sponge4

Like RC4, I need a 256-element byte array, and two 1-byte indices, i and j. Sponge4 also keeps a third 1-byte counter, k, to count input.

TYPE sponge4
    i AS INTEGER
    j AS INTEGER
    k AS INTEGER
    s(0 TO 255) AS INTEGER
END TYPE

QBasic doesn’t have a “byte” type. A fixed-size 256-byte string would normally be a good match here, but since they’re not arrays, strings are not compatible with SWAP and are not indexed efficiently. So instead I accept some wasted space and use 16-bit integers for everything.

There are four “methods” for this structure. Three are subroutines since they don’t return a value, but mutate the sponge. The last, squeeze, returns the next byte as an INTEGER (%).

DECLARE SUB init (r AS sponge4)
DECLARE SUB absorb (r AS sponge4, b AS INTEGER)
DECLARE SUB absorbstop (r AS sponge4)
DECLARE FUNCTION squeeze% (r AS sponge4)

Initialization follows RC4:

SUB init (r AS sponge4)
    r.i = 0
    r.j = 0
    r.k = 0
    FOR i% = 0 TO 255
        r.s(i%) = i%
    NEXT
END SUB

Absorbing a byte means running the RC4 key schedule one step. Absorbing a “stop” symbol, for separating inputs, transforms the state in a way that absorbing a byte cannot.

SUB absorb (r AS sponge4, b AS INTEGER)
    r.j = (r.j + r.s(r.i) + b) MOD 256
    SWAP r.s(r.i), r.s(r.j)
    r.i = (r.i + 1) MOD 256
    r.k = (r.k + 1) MOD 256
END SUB

SUB absorbstop (r AS sponge4)
    r.j = (r.j + 1) MOD 256
END SUB

Squeezing a byte may involve mixing the state first, then it runs the RC4 generator normally.

FUNCTION squeeze% (r AS sponge4)
    IF r.k > 0 THEN
        absorbstop r
        DO WHILE r.k > 0
            absorb r, r.k
        LOOP
    END IF

    r.j = (r.j + r.i) MOD 256
    r.i = (r.i + 1) MOD 256
    SWAP r.s(r.i), r.s(r.j)
    squeeze% = r.s((r.s(r.i) + r.s(r.j)) MOD 256)
END FUNCTION

That’s the entire generator in QBasic! A couple more helper functions will be useful, though. One absorbs entire strings, and the second emits 24-bit results.

SUB absorbstr (r AS sponge4, s AS STRING)
    FOR i% = 1 TO LEN(s)
        absorb r, ASC(MID$(s, i%))
    NEXT
END SUB

FUNCTION squeeze24& (r AS sponge4)
    b0& = squeeze%(r)
    b1& = squeeze%(r)
    b2& = squeeze%(r)
    squeeze24& = b2& * &H10000 + b1& * &H100 + b0&
END FUNCTION

QBasic doesn’t have bit-shift operations, so we must make due with multiplication. The &H is hexadecimal notation.

Putting the sponge to use

One of the problems with the original program is that only the time of day was a seed. Even were it mixed better, if we run the program at exactly the same instant on two different days, we get the same seed. The DATE$ function returns the current date, which we can absorb into the sponge to make the whole date part of the input.

DIM sponge AS sponge4
init sponge
absorbstr sponge, DATE$
absorbstr sponge, MKS$(TIMER)
absorbstr sponge, MKI$(ntickets)

I follow this up with the timer. It’s converted to a string with MKS$, which returns the little-endian, single precision binary representation as a 4-byte string. MKI$ does the same for INTEGER, as a 2-byte string.

One of the problems with the original program was bias: Multiplying RND by a constant, then truncating the result to an integer is not uniform in most cases. Some numbers are selected slightly more often than others because 2^24 inputs cannot map uniformly onto, say, 10 outputs. With all the shuffling in the original it probably doesn’t make a practical difference, but I’d like to avoid it.

In my program I account for it by generating another number if it happens to fall into that extra “tail” part of the input distribution (very unlikely for small ntickets). The squeezen function uniformly generates a number in 0 to N (exclusive).

FUNCTION squeezen% (r AS sponge4, n AS INTEGER)
    DO
       x& = squeeze24&(r) - &H1000000 MOD n
    LOOP WHILE x& < 0
    squeezen% = x& MOD n
END FUNCTION

Finally a Fisher–Yates shuffle, then print the first N elements:

FOR i% = ntickets - 1 TO 1 STEP -1
    j% = squeezen%(sponge, i% + 1)
    SWAP tickets(i%), tickets(j%)
NEXT

FOR i% = 1 TO nresults
    PRINT tickets(i%)
NEXT

Though if you really love Kris’s loop idea:

PRINT "Press Esc to finish, any other key for entropy..."
DO
    c& = c& + 1
    LOCATE 2, 1
    PRINT "cycles ="; c&; "; keys ="; k%

    FOR i% = ntickets - 1 TO 1 STEP -1
        j% = squeezen%(sponge, i% + 1)
        SWAP tickets(i%), tickets(j%)
    NEXT

    k$ = INKEY$
    IF k$ = CHR$(27) THEN
        EXIT DO
    ELSEIF k$ <> "" THEN
        k% = k% + 1
        absorbstr sponge, k$
    END IF
    absorbstr sponge, MKS$(TIMER)
LOOP

If you want to try it out for yourself in, say, DOSBox, here’s the full source: sponge4.bas

Have a comment on this article? Start a discussion in my public inbox by sending an email to ~skeeto/public-inbox@lists.sr.ht [mailing list etiquette] , or see existing discussions.