Unintuitive JSON Parsing

This article was discussed on Hacker News and on reddit.

Despite the goal of JSON being a subset of JavaScript — which it failed to achieve (update: this was fixed) — parsing JSON is quite unlike parsing a programming language. For invalid inputs, the specific cause of error is often counter-intuitive. Normally this doesn’t matter, but I recently ran into a case where it does.

Consider this invalid input to a JSON parser:

[01]

To a human this might be interpreted as an array containing a number. Either the leading zero is ignored, or it indicates octal, as it does in many languages, including JavaScript. In either case the number in the array would be 1.

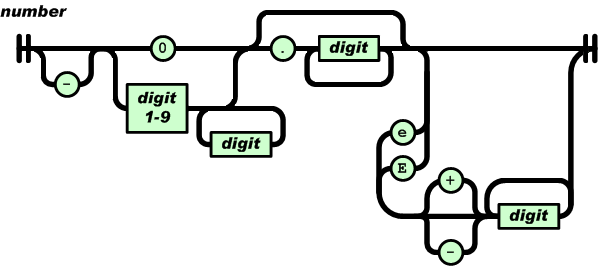
However, JSON does not support leading zeros, neither ignoring them nor supporting octal notation. Here’s the railroad diagram for numbers from the JSON specficaiton:

Or in regular expression form:

-?(0|[1-9][0-9]*)(\.[0-9]+)?([eE][+-]?[0-9]+)?

If a token starts with 0 then it can only be followed by ., e, or E. It cannot be followed by a digit. So, the natural human response to mentally parsing [01] is: This input is invalid because it contains a number with a leading zero, and leading zeros are not accepted. But this is not actually why parsing fails!

A simple model for the parser is as consuming tokens from a lexer. The lexer’s job is to read individual code points (characters) from the input and group them into tokens. The possible tokens are string, number, left brace, right brace, left bracket, right bracket, comma, true, false, and null. The lexer skips over insignificant whitespace, and it doesn’t care about structure, like matching braces and brackets. That’s the parser’s job.

In some instances the lexer can fail to parse a token. For example, if while looking for a new token the lexer reads the character %, then the input must be invalid. No token starts with this character. So in some cases invalid input will be detected by the lexer.

The parser consumes tokens from the lexer and, using some state, ensures the sequence of tokens is valid. For example, arrays must be a well formed sequence of left bracket, value, comma, value, comma, etc., right bracket. One way to reject input with trailing garbage, is for the lexer to also produce an EOF (end of file/input) token when there are no more tokens, and the parser could specifically check for that token before accepting the input as valid.

Getting back to the input [01], a JSON parser receives a left bracket token, then updates its bookkeeping to track that it’s parsing an array. When looking for the next token, the lexer sees the character 0 followed by 1. According to the railroad diagram, this is a number token (starts with 0), but 1 cannot be part of this token, so it produces a number token with the contents “0”. Everything is still fine.

Next the lexer sees 1 followed by ]. Since ] cannot be part of a number, it produces another number token with the contents “1”. The parser receives this token but, since it’s parsing an array, it expects either a comma token or a right bracket. Since this is neither, the parser fails with an error about an unexpected number. The parser will not complain about leading zeros because JSON has no concept of leading zeros. Human intuition is right, but for the wrong reasons.

Try this for yourself in your favorite JSON parser. Or even just pop up the JavaScript console in your browser and try it out:

JSON.parse('[01]');

Firefox reports:

SyntaxError: JSON.parse: expected ‘,’ or ‘]’ after array element

Chromium reports:

SyntaxError: Unexpected number in JSON

Edge reports (note it says “number” not “digit”):

Error: Invalid number at position:3

In all cases the parsers accepted a zero as the first array element, then rejected the input after the second number token for being a bad sequence of tokens. In other words, this is a parser error rather than a lexer error, as a human might intuit.

My JSON parser comes with a testing tool that shows the token stream up until the parser rejects the input, useful for understanding these situations:

$ echo '[01]' | tests/stream
struct expect seq[] = {
    {JSON_ARRAY},
    {JSON_NUMBER, "0"},
    {JSON_ERROR},
};

There’s an argument to be made here that perhaps the human readable error message should mention leading zeros, since that’s likely the cause of the invalid input. That is, a human probably thought JSON allowed leading zeros, and so the clearer message would tell the human that JSON does not allow leading zeros. This is the “more art than science” part of parsing.

It’s the same story with this invalid input:

[truefalse]

From this input, the lexer unambiguously produces left bracket, true, false, right bracket. It’s still up to the parser to reject this input. The only reason we never see truefalse in valid JSON is that the overall structure never allows these tokens to be adjacent, not because they’d be ambiguous. Programming languages have identifiers, and in a programming language this would parse as the identifier truefalse rather than true followed by false. From this point of view, JSON seems quite strange.

Just as before, Firefox reports:

SyntaxError: JSON.parse: expected ‘,’ or ‘]’ after array element

Chromium reports the same error as it does for [true false]:

SyntaxError: Unexpected token f in JSON

Edge’s message is probably a minor bug in their JSON parser:

Error: Expected ‘]’ at position:10

Position 10 is the last character in false. The lexer consumed false from the input, produced a “false” token, then the parser rejected the input. When it reported the error, it chose the end of the invalid token as the error position rather than the start, despite the fact that the only two valid tokens (comma, right bracket) are both a single character. It should also say “Expected ‘]’ or ‘,’” (as Firefox does) rather than just “]”.

Concatenated JSON

That’s all pretty academic. Except for producing nice error messages, nobody really cares so much why the input was rejected. The mismatch between intuition and reality isn’t important.

However, it does come up with concatenated JSON. Some parsers, including mine, will optionally consume multiple JSON values, one after another, from the same input. Here’s an example from one of my favorite command line tools, jq:

echo '{"x":0,"y":1}{"x":2,"y":3}{"x":4,"y":5}' | jq '.x + .y'
1
5
9

The input contains three unambiguously-concatenated JSON objects, so the parser produces three distinct objects. Now consider this input, this time outside of the context of an array:

01

Is this invalid, one number, or two numbers? According to the lexer and parser model described above, this is valid and unambiguously two concatenated numbers. Here’s what my parser says:

$ echo '01' | tests/stream
struct expect seq[] = {
    {JSON_NUMBER, "0"},
    {JSON_DONE},
    {JSON_NUMBER, "1"},
    {JSON_DONE},
    {JSON_ERROR},
};

Note: The JSON_DONE “token” indicates acceptance, and the JSON_ERROR token is an EOF indicator, not a hard error. Since jq allows leading zeros in its JSON input, it’s ambiguous and parses this as the number 1, so asking its opinion on this input isn’t so interesting. I surveyed some other JSON parsers that accept concatenated JSON:

• Jackson: Reject as leading zero.
• Noggit: Reject as leading zero.
• yajl: Accept as two numbers.

For my parser it’s the same story for truefalse:

echo 'truefalse' | tests/stream
struct expect seq[] = {
    {JSON_TRUE, "true"},
    {JSON_DONE},
    {JSON_FALSE, "false"},
    {JSON_DONE},
    {JSON_ERROR},
};

Neither rejecting nor accepting this input is wrong, per se. Concatenated JSON is outside of the scope of JSON itself, and concatenating arbitrary JSON objects without a whitespace delimiter can lead to weird and ill-formed input. This is all a great argument in favor or Newline Delimited JSON, and its two simple rules:

1. Line separator is '\n'
2. Each line is a valid JSON value

This solves the concatenation issue, and, even more, it works well with parsers not supporting concatenation: Split the input on newlines and pass each line to your JSON parser.

• javascript
• compsci
• lang